레포트 컴퓨터물리학 - 메트랩

레포트 컴퓨터물리학 - 메트랩

[레포트] 컴퓨터물리학 - 메트랩.hwp

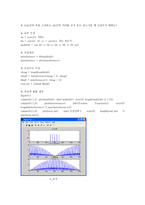
본문 % i)slit간의 폭을 고정하고 slit간의 거리를 증가 또는 감소시킬 때 간섭무늬 변화는? % 슬릿 구성 aa = zeros(1, 500); bb = ones(1, 2); cc = zeros(1, 50); %증가 multislit = aa bb cc bb cc bb cc bb cc bb aa ; % 간섭계산 interference = fft(multislit); interference = abs(interference); % 간섭무늬 구성 sleng = length(multislit); rrhalf = interference(sleng / 2: sleng); llhalf = interference(1: sleng / 2); real_int = rrhalf llhalf ; % 푸리에 변환 결과 figure(1) subplot(3,1,1); plot(multislit); title(multislit); axis( 0 length(multislit) 0 1.5 ); subplot(3,1,2); plot(interference); title(Fourier Transform); axis( 0 length(interference) 0 max(interference) ); subplot(3,1,3); plot(real_int); title(간섭진폭); axis( 0 length(real_int) 0 max(real_int) ); i)_증가 % i)slit간의 폭을 고정하고 slit간의 거리를 증가 또는 감소시킬 때 간섭무늬 변화는? % 슬릿 구성 aa = zeros(1, 500); bb = ones(1, 2); cc = zeros(1, 10); %감소 multislit = aa bb cc bb cc bb cc bb cc bb aa ; % 간섭계산 interference = fft(multislit); interference = abs(interference); % 실제에 맞게 간섭무늬 구성 sleng = length(multislit); rrhalf = interference(sleng / 2: sleng); llhalf = interference(1: sleng / 2); real_int = rrhalf llhalf ; % 푸리에 변환 결과 figure(1) subplot(3,1,1); plot(multislit); title(multislit); axis( 0 length(multislit) 0 1.5 ); subplot(3,1,2); plot(interference); title(Fourier Transform); axis( 0 length(interference) 0 max(interference) ); subplot(3,1,3); plot(real_int); title(간섭진폭); axis( 0 length(real_int) 0 max(real_int) ); i)_감소 % ii)slit간의 거리를 고정하고 slit 폭을 증가시킬 때 간섭무늬 변화는? % 슬릿 구성 aa = zeros(1, 500); bb = ones(1, 30); cc = zeros(1, 30); multislit = aa bb cc bb cc bb cc bb cc bb aa ; % 간섭계산 interference = fft(multislit); interference = abs(interference); % 실제에 맞게 간섭무늬 구성 sleng = length(multislit); rrhalf = interference(sleng / 2: sleng); llhalf = interference(1: sleng / 2); real_int = rrhalf llhalf ; % 푸리에 변환 결과 figure(1) subplot(3,1,1); plot(multislit); title(multislit); axis( 0 length(multislit) 0 1.5 ); subplot(3,1,2); plot(interference); title(Fourier Transform); axis( 0 length(interference) 0 max(interference) ); subplot(3,1,3); plot(real_int); title(간섭진폭); axis( 0 length(real_int) 0 max(real_int) ); ii) % iii)slit폭과 slit거리를 고정하고 slit 수를 증가시킬 때 간섭무늬 변화는? % 슬릿 구성 aa = zeros(1, 1000); bb = ones(1, 30); cc = zeros(1, 30); multislit = aa bb cc bb cc bb cc bb cc bb aa ; % 간섭계산 interference = fft(multislit); interference = abs(interference); % 실제에 맞게 간섭무늬 구성 sleng = length(multislit); rrhalf = interference(sleng / 2: sleng); llhalf = interference(1: sleng / 2); real_int = rrhalf llhalf ; % 푸리에 변환 결과 figure(1) subplot(3,1,1); plot(multislit); title(multislit); axis( 0 length(multislit) 0 1.5 ); subplot(3,1,2); plot(interference); title(Fourier Transform); axis( 0 length(interference) 0 max(interference) ); subplot(3,1,3); plot(real_int); title(간섭진폭); axis( 0 length(real_int) 0 max(real_int) ); iii) 하고 싶은 말 좀 더 업그레이드하여 자료를 보완하여, 과제물을 꼼꼼하게 정성을 들어 작성했습니다. 위 자료 요약정리 잘되어 있으니 잘 참고하시어 학업에 나날이 발전이 있기를 기원합니다 ^^ 구입자 분의 앞날에 항상 무궁한 발전과 행복과 행운이 깃들기를 홧팅 키워드 간섭, 구성, 결과, 변환, 간섭진폭, 무늬